近日,西北大学物理学院经光银教授与合作者围绕微游泳体与流场的相互作用,从物理视角通过实验、数值计算、理论定义了具有左手螺旋鞭毛主导的游泳流体力学效应,构建了游动细菌的偏航全景图,解决了如何精确描述基本生物体准确轨迹这一长期困扰生物物理领域的难题。研究成果以“Chirality-induced bacterial rheotaxis in bulk shear flows”为题,于7月10日发表在Science子刊Science Advances。

日常生活中,无驱动力的物体只能随波逐流,例如,皮球在流动水面上跟随流水,漂流而下的细长竹筏尽管旋转但质心仍顺流而下。从物理角度来看,这些物体的运动具有一个共同特征,即物体质心顺着流体的流线前行,而不能横向跨越流线,从而制约这些“被动”物体的精准递送,尤其在小尺度下定点输运是一个巨大挑战。然而如果这些物体具有自驱动、自响应及自适应的“自我意识”,则必将改变被动式的输运行为,我们将这类物体称为自驱动物质。
这类自驱动物质持续不断地将能量以不同形式转化为机械运动,生命活动中绝大多数过程包含了这类物质的主动运动与输运。1940年代伟大的量子物理学家薛定谔在《生命是什么》中提出了一个很有启发的问题,即为什么原子如此之小,而我们的身体需要如此之大?显然,原子、分子热运动(布朗运动)让微小世界变得杂乱无章,生命体需要一定的宏观尺寸才能克服这种随机干扰,小尺度下的热运动是被动/主动物体精准定位运动的重要障碍。
近20年来,活性生物物理开始成为物理学新兴前沿研究领域,这类系统显著区别常规平衡态物理,系统在微观单元上有能量输入而被推向远离平衡态,其中微单元体具有自驱动、自适应,且可在无序中生有序并产生集群行为。受到应用需求刺激,在小尺度(如毫米以下)定位导航、精准外科手术、药物释放、微尺度下物质输送、微纳机器人研制等,对运动单元在无序复杂微环境介质中定向运动与导航具有重大应用价值。
细菌作为一种天然“自驱动粒子”,其运动支撑着许多微观与宏观生命活动,研究细菌运动规律,对细胞、细菌等在微管道中分离与分类、设计功能性生物马达、微机器人、以及防治微生物污染、细菌感染等提供科学依据。大肠杆菌是由一束左手螺旋鞭毛以约100赫兹逆时针转动,通过反作用力在流体中获得推力,以20~30微米每秒速度游动,当部分鞭毛反转时,细菌便转弯或转身,从而可类比于主动布朗粒子,依赖这种“低效”的扩散模式探索它们赖以生存的空间来觅食或逃生。显然,正如理论物理学家薛定谔指出的原子、分子热运动(布朗运动)让微小世界变得杂乱无章,需要借助外力驱使微粒做定向运动。
从物理角度来看,构造一个具有空间不均匀的梯度场是个不错的想法。于是趋化性、驱热、趋光、趋磁、趋重力等效应在微生物的定向运动中备受关注。而驱流性(Rheotaxis)近年来才开始受到重视。由于细菌作为一类微游泳体(Microswimmer),微米尺度的身材使得布朗运动主导其游动的随机取向。流场可以产生应力作用于细菌整个表面,我们不禁好奇,做游泳运动的细菌是否在流速梯度场中展示出特殊的游动行为,是否能逃脱“随波逐流”的命运,而采取“智慧式”的响应与自适应行为?
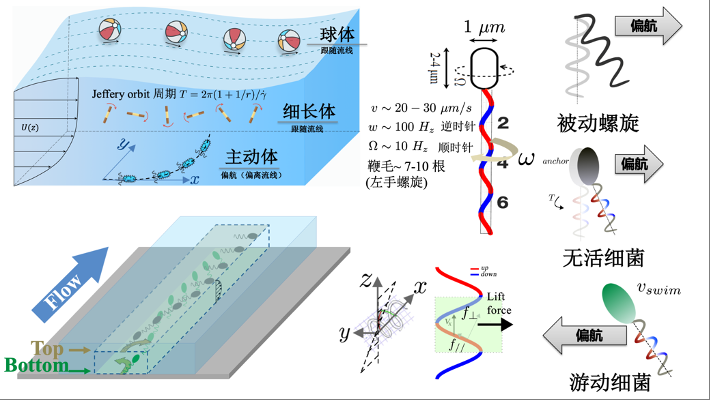
图1 被动物体跟随流线示意图,以及左手螺旋、被动螺旋游泳体、活性螺旋细菌感受流场剪切力的运动力学机制示意图。管道底部细菌往左偏航,顶部细菌往右偏航。
2012年R. Stocker在MIT的课题组首次报道了具有手性细菌在剪切流中出现横向运动,然而这种横向“过河”运动与流场、布朗热运动、活性噪声、细菌取向等具有何种本质的物理机制都尚未明确。基于此,研究团队构建了一个精细的细菌显微跟踪实验,结合数值模拟,建立了精确流体物理模型,揭示了这种手性细菌驱流性的物理规律。
实验上,通过高速显微精确成像,团队测量了微流管道中细菌轨迹、速度大小与取向,获得了大量细菌运动统计结果,如图2所示,展示了细菌在流场究竟如何游动的精细细节。发现跨越流线的横向速度随着局域剪切率增加而增加,即管道中流量越大,细菌越容易做横向游动;越接近管道壁面(高剪切率)横向运动越显著。
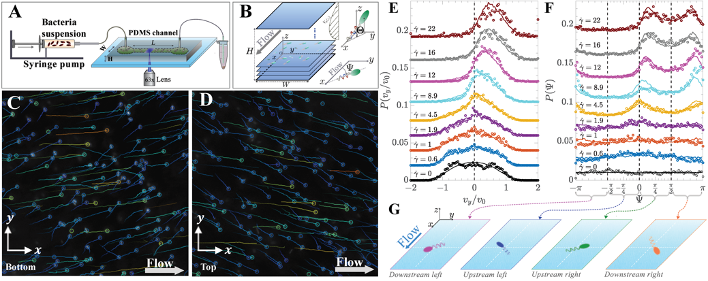
图2 细菌在微流管道中的游动规律。(A)与(B)为微流管道中细菌显微成像示意图;(C)与(D)为细菌在管道的底部与顶部偏离流线而分别向左与向右(顺着流场方向观察);(E-G)为细菌横向速度与导航角在不同剪切率下概率分布及偏航示意图。
物理上,细菌头部可看作细长的椭球,在剪切流场中会做经典的周期Jeffery轨道运动,即一边跟随流场被动输运,一边绕自身质心做周期运动,考虑热噪声与细菌主动运动,团队写出了速度与方向矢量演化方程
。这里一个巨大挑战是,如何确立鞭毛手性引起的细菌方向矢量变化?团队凭借多年的研究经验与物理直觉推测出了此作用项,从而得到了实验、模拟、理论惊人的一致结果见图2E-F,建立了手性引起细菌运动驱流普适方程与规律。
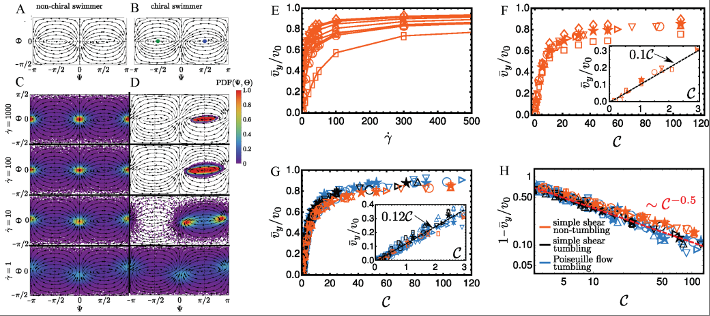
图3 Jeffery轨道运动与手性引起的驱流运动竞争机制。(A-B)给出了无手性的周期性Jeffery轨道运动与细菌手性引起的偏航游动;(C)展示不同剪切流场作用下手性引起的偏航稳定性相图,手性驱流迫使细菌趋于不稳定的不动点。(D)考虑不同控制参数剪切率、噪声强度、流场类型、手性强度等,最后(E-H)通过定义一个全新的无量纲“手性”数(Chirality number),获得了驱流运动的普适标度律。
在此之前,一直困扰着人们的一个问题是,如果剪切流场对手性粒子产生横向合力,那么当流场非常大时,细菌是否完全以90度角横向“过河”?对此,实验上存在挑战,理论上又由于无法解析地给出手性作用项而变得无能为力。团队认为这个手性作用项的表达式,可以定量描述细菌驱流的稳态动力学过程,在理论上重构了手性粒子在流场中运动的全景图。
团队首次定义了一个新的无量纲数,即“手性”数(Chirality number),获得了驱流运动的普适标度律。有趣的是,这是否意味着,如果考虑所有已知因素,细菌进入管道后,是否就可预测,在管道出口处细菌以何种形式、从什么地方游出吗,即预测它们的部分人生轨迹?
答案跟前面薛定谔提出的问题类似,这一切不确定性来源于热噪声与细菌进化所形成的随机游动性,很难精确控制并诱使哪怕如此基本生物体的准确轨迹,这也是微纳马达机器人研究领域所要克服的难题。
经光银教授作为论文第一作者,西北大学为第一完成单位,合作者包括巴黎物理化学学院(ESPCI)的Eric Clément、Anke Lindner教授和维也纳技术大学的Andreas Zöttl博士。该项工作受到国家自然科学基金面上项目(11774287)资助。